Are CFO's Men with Hammers?
I often ask my students the following question:
You are the CFO of a textile company which makes commodity yarn. The industry in which you operate is extremely competitive beset with excess capacity.
A leading textile machinery manufacturer’s marketing agent approaches you with a proposal to sell you a new loom which is more efficient than any other loom available in the market. He informs you that the new invention is far more efficient and that it will save your company a substantial sum of money every year, so that it will pay for itself in a very short span of time. To justify his claims, he presents you with the following figures: (1) Cost of machine: $100 million.; (2) expected life = 10 years; (3) annual savings in operating costs for the next 10 years = $25 million. p.a.; (4) expected residual value of the machine = $10 million.
You have verified the numbers presented to you and find them to be accurate. Your company’s pre-tax hurdle rate is 15% p.a.
Should your company place orders to buy these looms?
Using their newly-acquired skills in DCF analysis, the students quickly determine the NPV, which is large and positive, and conclude that the loom should be purchased and installed as soon as possible.
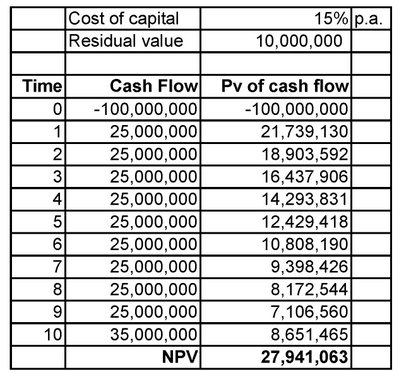
The main problem with this approach is that it often leads to wrong conclusions arising out of over-use of the DCF model in finance and ignorance of appropriate models from other disciplines such as microeconomics, game theory, and psychology.
Warren Buffett, the world’s most respected investor and Chairman of Berkshire Hathaway Inc., and his partner, Charlie Munger, call this “the man with a hammer syndrome”: To a man with a hammer everything looks like a nail. If all you have is one tool, you’re going to end up overusing it.
How can one deal with the man with a hammer syndrome? Well, the best way, according to Mr. Munger, is to train oneself to “jump jurisdictional boundaries” and grab the most appropriate models from multiple disciplines that best solve the problem at hand.
The present problem requires a two-step analysis drawing on models from multiple disciplines before drawing any conclusions.
The first step involves using DCF analysis, which my students have no problem with. That part of the analysis has already been done and described above.
It’s the second part of the analysis which they miss. They miss it because they are not yet trained to think in a multi-disciplinary manner.
That second part of the analysis requires them to answer the following question: How much of the cost savings that the new loom will deliver be kept by the company and how much of it will be passed on to the company’s customers?
Ah ha! Now it gets a bit tricky, doesn’t it? It gets tricky because to answer that question one has to grab models from microeconomics – such as the model of competition. And, of course, when you look at it from that angle, its obvious, that given the nature of textile industry’s competitive nature, arising out of surplus capacity and commodity attributes of the product, most of the cost-savings from the new loom will go to the customers of the company, and not to its owners.
This will happen because once a textile company acquires the new loom and achieves the promised cost savings, it will tend to either lower its prices to gain market share, or keep prices unchanged to earn higher margins.
Sooner or later either of these two actions would get noticed by the company’s competitors and they would naturally rush to make the same investments in new, efficient looms, in order to regain lost market share or to earn higher margins. Ironically, the very salesman who sold the loom to your textile company will rush to sell it to your second competitor and then the third one and so on, citing your own cost saving experience as reason for your competitors to buy his company’s new invention. After all, he is not in the business to make your production process more efficient. He is in the business of making money for his company (“Whose bread I eat, his song I sing”).
In our problem, competition i.e. the absence of a cartel will ensure that almost all of the efficiency gains end up in the pockets of the buyers of textiles, and not in the pockets of the owners of the textile companies.
Another irony arises out of the fact that this tragic outcome would occur even though all of the promised efficiency gains materialized. It’s not that the new looms aren’t any good. In fact they are so good that any advantage for the early buyers will prove to be a temporary illusion because sooner or later everyone has to have one or risk being perished.
Such is the nature of certain businesses where you have to keep on putting more and more money in just to stay where you are. (It's like running up on an escalator which is moving down - lots of investment, zero progress). You keep on investing money in projects which have positive NPVs and high IRRs and still end up earning substandard returns on capital that destroy shareholder value.
On the other hand, if we were dealing with India's largest tobacco company like ITC, a virtual monopoly where the buyers of its cigarettes are price-insensitive addicts – if someone sold it a more efficient machine to make its cigarettes - then the cost savings from this new wonderful invention will not be passed on to the customers. Rather, much of the post-tax cost savings would accrue to the benefit of ITC’s shareholders.
So, without jumping over the jurisdictional boundary of finance where DCF resides, into the jurisdictional boundary of microeconomics where the model of competition resides, you cannot solve the problem at hand in a satisfactory manner.
In early 1980s, Mr. Buffett faced a similar dilemma in the management of the unprofitable textile business of Berkshire Hathaway. He knew that the US textile industry was going to become increasingly uncompetitive, primarily due to its high, and impossible to reduce, labor costs. He also knew that he had other opportunities in which he could invest capital where the prospects of earning superior returns were excellent, given the fundamental economics of those businesses then available.
Long before most capitalists would even consider the possibility, in 1985, Mr. Buffett decided to shut down the textile operations of Berkshire and redeploy the capital in great businesses. It proved to be one of the best business decisions he ever made. In a letter written to the shareholders of Berkshire in 1985, Mr. Buffett reasoned:
“The promised benefits from these textile investments were illusory. Many of our competitors, both domestic and foreign, were stepping up to the same kind of expenditures and, once enough companies did so, their reduced costs became the baseline for reduced prices industry wide. Viewed individually, each company’s capital investment decision appeared cost effective and rational; viewed collectively; the decisions neutralized each other and were irrational (just as happens when each person watching a parade decides he can see a little better if he stands on tiptoes). After each round of investment, all the players had more money in the game and returns remained anemic.”
Mr. Buffett utilized the metaphor of a parade to illustrate a well-known problem in game theory called “Prisoner’s Dilemma.”
Prisoner’s dilemma involves two suspects, A and B, who have been arrested by the police. The police have insufficient evidence for a conviction, and, after separated both prisoners, offer each the same deal: if one testifies for the prosecution against the other and the other remains silent, the betrayer goes free and the silent accomplice receives the full 10-year sentence. If both stay silent, the police can sentence both prisoners to only six months in jail for a minor charge. If each betrays the other, each will receive a two-year sentence. Each prisoner must make the choice of whether to betray the other or to remain silent. However, neither prisoner knows for sure what choice the other prisoner will make. So the question this dilemma poses is: What will happen? How will the prisoners act? The dilemma is summarized in the following table:

The dilemma arises when one assumes that both prisoners only care about minimizing their own jail terms. Each prisoner has two options: to cooperate with his accomplice and stay quiet, or to defect from their implied pact and betray his accomplice in return for a lighter sentence. The outcome of each choice depends on the choice of the accomplice, but the player must choose without knowing what their accomplice has chosen to do.
Let's assume prisoner A is working out his best move. If his partner stays quiet, his best move is to betray as he then walks free instead of receiving the minor sentence. If his partner betrays, his best move is still to betray, as by doing it he receives a relatively lesser sentence than staying silent. At the same time, the other prisoner's thinking would also have arrived at the same conclusion and would therefore also betray.
If reasoned from the perspective of the optimal outcome for the group (of two prisoners), the correct choice would be for both prisoners to cooperate with each other, as this would reduce the total jail time served by the group to one year total. Any other decision would be worse for the two prisoners considered together. When the prisoners both betray each other, each prisoner achieves a worse outcome than if they had cooperated.
In other words, actions that appear to be rational from an individual’s perspective sometimes become foolish, when viewed from a group’s perspective. The functional equivalent of the prisoner’s dilemma in our problem creates miserable choices but would we have discovered that unless we had jumped over into the jurisdictional boundary of game theory? I think not.
So, we grabbed DCF from finance, and then jumped over its jurisdictional boundary into the territory called microeconomics, where we grabbed competition. Then we jumped over the fence again and grabbed prisoner’s dilemma from game theory.
We need one more jump into the jurisdiction of psychology. And then we can stop jumping around and solve the problem.
One model we will grab from psychology is what Mr. Munger calls “bias from commitment and consistency.” When you have already made prior commitments to pet projects, you may find it hard, even impossible, to reverse your position and change course. If old reasons are no longer valid to support the original decision, new ones shall be invented. Man, after all, is not a rational animal, but a rationalizing one.
Another model we will grab from psychology is called the “contrast effect”. One version of the contrast effect makes small, incremental escalations in commitments go un-noticed, particularly when these escalations are carried out over a long period of time.
It works in Chinese brainwashing techniques. It also contributes to foolish business decisions.
If you’ve already sunk in $1oo million in a bad capital investment project, an additional investment of $10 million will look very small in contrast to the much bigger total commitment already made and will therefore tend to go un-noticed.
This version of contrast effect is also called the "boiling frog syndrome": If you put a frog in boiling hot water, it will jump out instantly, but if you put a frog in room-temperature water and then slowly heat it, it will boil and die.
The story about the boiling frog isn’t true. That metaphor, however, is highly appropriate because the human equivalent of the boiling frog is there in all of us.
Mr. Buffett could see that bias from commitment and consistency and the boiling frog syndrome from psychology often combine with the prisoners’ dilemma model from game theory, making many a businessman take foolish decisions by continuing to sink more and more money in a lousy business instead of taking money out and re-deploying it more productively elsewhere. He realized that in some industries the chief problem is that if you continue to remain in the game then “you can’t be a lot smarter than your dumbest competitor”.
And, so, Mr. Buffett wisely refused to play this game and withdrew his capital from the textile business and re-invested the proceeds in businesses with much better fundamental economics like Coke, Gillette, Capital Cities, See’s Candies, and Nebraska Furniture Mart. Over time, his decisions to shut down the textile operations of Berkshire and to re-allocate the released capital elsewhere have made its shareholders richer by tens of billions of dollars.
Mr. Buffett’s multi-disciplinary mind helped him solve a complex business problem. I see no reason why CFOs cannot apply the same thinking style in solving complex business problems they face.
Otherwise, they are destined to remain as “men with hammers”.
